
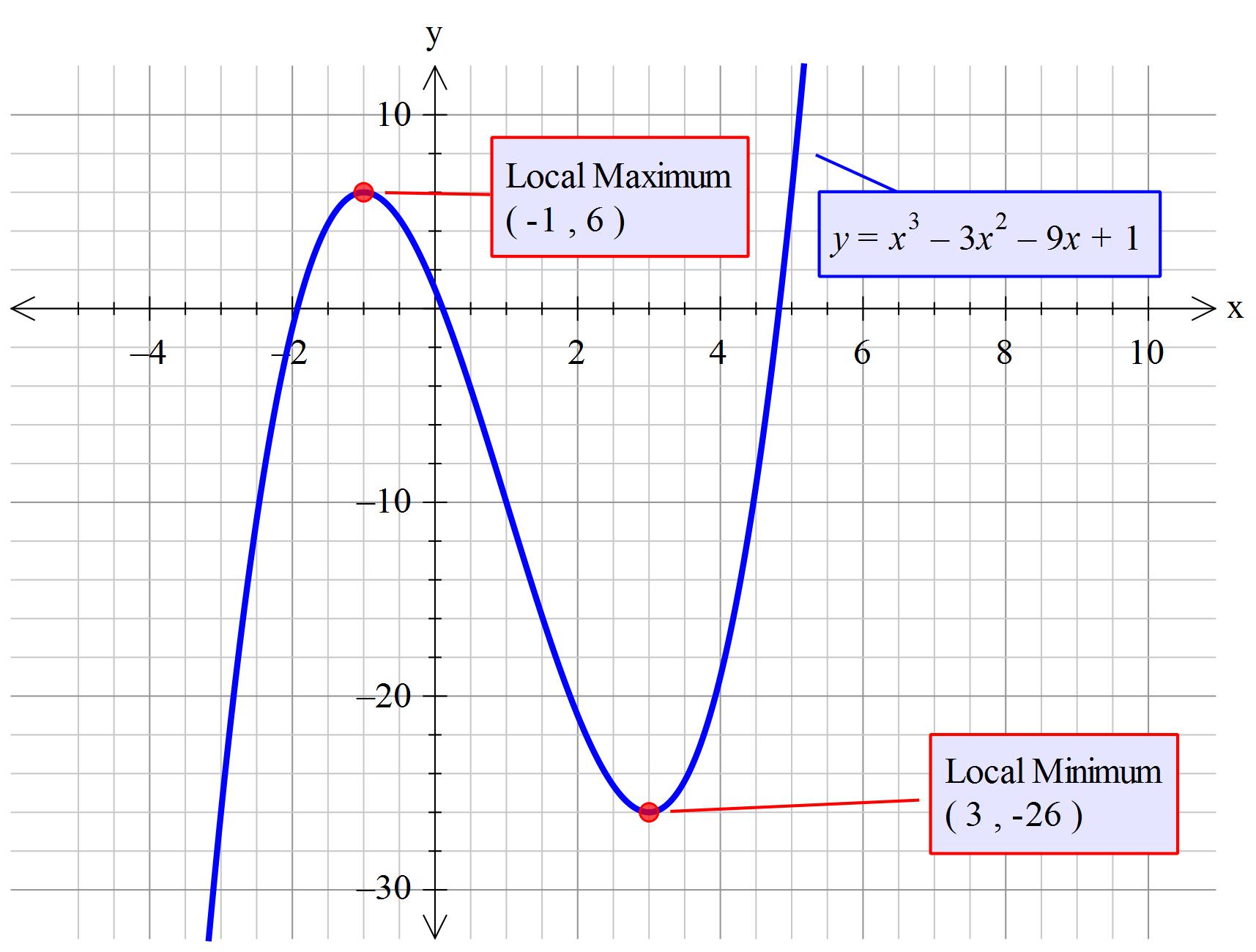
So, the x-intercepts of the function are at 1, 3, and 0.5.Īs shown in Figure 06, after completing Step 1 by finding the y-intercept and the x-intercepts, you know that the cubic function graph will pass through the points (0,3), (-3,0), (0.5,0), and (1,0). Now the solutions to the equation become more apparent and can be obtained by equating each factor to 0.
It is easier to determine the roots of this cubic function by first factorizing the equation as shown below: To find the x-intercepts, figure out the value of the function when f(x)=0 as follows: So, t he y-intercept of the cubic function is at 3. Let’s go ahead and apply these three steps to the given function f(x) = 2x^3 + 3x^2 - 8x +3 as follows: Step 1: Identify the intercepts To graph a cubic function like the one given in this first example, you can use the following 3-step method: In a cubic function given by f(x) =, the inflection point is given by x=-b/3aįigure 03 below illustrates examples of critical points and an inflection point on a cubic function graph.Įxample #1: Graph f(x) = 2x^3 + 3x^2 - 8x +3 Point of inflection: This is the point where the concavity of the curve changes direction. To obtain these points, you need to obtain the derivative f’(x) and solve for f’(x) = 0. The y-intercept is the value of the function when x = 0, i.e f(0).Ĭritical points: The local maximum and minimum points, also known as stationary points, are points on the graph where the gradient of the function is 0. X and y -intercepts: The x-intercepts, also known as the roots of the function, can be determined by finding the solutions to f(x) = 0. When graphing a cubic function it is essential to determine the following key features and behaviors of the function. Notice that the cubic function graph as three real roots (x-intercepts) and two critical points (a local maximum and a local minimum). Some features that distinguish cubic functions from linear and quadratics are:Ī cubic function graph has either one or three real roots (x-intercept/s)Ī cubic function graph may have two critical points, a local maximum, and a local minimumĪ cubic function graph has a single inflection pointįigure 02 shows the end result of graphic a cubic function with equation f(x)=x^3-4x^2+5. Linear functions have one root, quadratics have a maximum of 2 roots, and 3rd-degree functions, cubic functions, have a maximum of 3 roots. The maximum number of roots (solutions to f(x) = 0) is the same as the degree of the function. Since both the domain and range span the set of real numbers, there are no vertical or horizontal asymptotes

The domain is the set of all real numbers Let’s start by comparing the parent graphs of the linear function graph (1st-degree), quadratic function graph (2nd-degree), and cubic-function graph (3rd-degree) as shown in Figure 01 below.
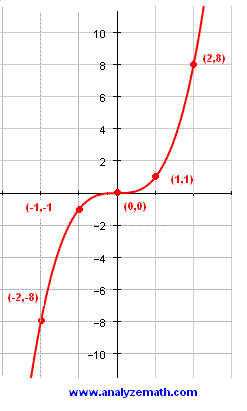
By the end of this guide, you'll have the skills to graph cubic functions and gain a deeper understanding of their behavior. Graphing a cubic function has similarities to linear and quadratic functions, however, cubic functions have unique characteristics that will be explored in this guide. After you’ve learned about graphing linear and quadratic functions, cubic functions are the next obvious step. What does a cubic function graph look like?Ĭubic functions are polynomials that are 3rd-degree functions and appear a lot when studying polynomials. This complete guide will explore and answer the following: Unlike graphing a parabola that represents a 2nd-degree function, a cubic function graph has it’s own unique shape and characteristics. Graphing a cubic function is an algebra skill that requires you to draw a graph that represents a 3rd-degree function on the coordinate plane.


 0 kommentar(er)
0 kommentar(er)
